A Simple Calculation That Could Change the Way You Think About Investing

This article is about Bear Market Probability and how to calculate it. As is my custom, I begin with a quote from the Rock ‘N Roll Archives:

The question to everyone’s answer
Is usually asked from within.

-The Steve Miller Band

What are the odds?

Ask an accomplished investor or a world-class poker player to list the most critical skills it takes to be a consistent winner. Common answers might include hard work, situational awareness, sound money management, a set of rules and the discipline to stick to them, and the ability to read your opponents.

But the #1 skill these elite players cite is the ability to calculate the odds of winning or losing on any hand, any bet, any trade, or any strategy. Commonly known as the risk/reward ratio, investors and gamblers who can do the calculation have a distinct advantage over those who can’t.

We know three things about the market with nearly 100% certainty:

1. This historic bull market will come to an end someday.
2. There will be another bear market, and it’s coming closer every day.
3. Nobody knows precisely when either of these things will happen.

The relationship between risk and reward is a cornerstone of Modern Portfolio Theory. It’s an easy concept to grasp – the greater the risk, the greater the reward – but how do you measure these two things? As it turns out, it’s not rocket science.

The reward part is easy. The stock market churns out a 10% annual reward, on average. So just sit back and enjoy the ride. But the risk part is way harder. What, if anything, should you do when the market hits a rough patch? Thankfully, most of the bumps along the way will be mild and brief. That is, until the next big one arrives (a technical term).

Nobody knows if the next drop will be one of the mild ones, or the beginning of a serious bear market. In the mother of all bear markets – the crash of 1929 –  investors lost 80% of their savings. It took 28 years for them to make it all back. At least half of them died before they got even.

More than anything else, investing is about managing downside risk

Let’s start with the obvious – what is risk? Most financial experts and academic types say that risk is the price volatility of an investment. There’s some truth to that, because wild price swings feel risky. But there’s an even more important aspect of risk… the chance of suffering a permanent loss of capital.

Every stock, bond, or fund you buy must be sold eventually, (or become worthless, or get bought out or merged into another entity). At that point in time there is a terminal wealth calculation. How much you got when you sold it, minus how much you spent when you bought it. If the difference between these two amounts is less than zero, you have just suffered a permanent loss of capital that you can never get back no matter how long you live. That is what I call true risk.

Your competitive advantage

If you understand how probability works in the context of the stock market, congratulations. You have a competitive advantage over investors who don’t know how to calculate them, or simply don’t bother to do the work.

The good news is that it isn’t very hard to work out probabilities in the investment realm. What it takes is common sense, a bit of logic, and the willingness to test your first instinct to see if it passes the smell test. The rest of this article will explain, with examples, how to do that.

We’ll start with the widest lens, which is the entire history of stock prices going back to 1941. We could have gone back even farther, but we decided to avoid the worst part of the Great Depression era, because the losses were so pervasive that they skewed the results too far to the negative. Starting in 1941 still encompasses a large part of those dark days in the market, and World War II, which we believe gives us a realistic picture of market behavior in good times and bad.

The first step in calculating probability is to ask the right questions

Before we can calculate the odds, we need to spell out what we’re looking for. In this article, we want to know the odds that a bear market is approaching. It’s an important question. Who wants to be the last one to jump in, just before a crash? We already know that it’s virtually guaranteed that a bear market is coming someday, so we need to narrow our time frame to make it practical. I chose two time frames: 12 months, and 24 months.

If I knew that there was a 90% probability a bear market was coming sometime in the next 12 months, I would take steps to protect my life savings. But if the probability was only 25%, I would probably stay fully invested.

Let’s widen the time frame to the next 24 months. If the probability of a bear market was 90%, I would take different steps to protect my savings. At first, I would slow down my new purchases. Next, I would stop putting new money into the market entirely. And finally, I would begin to reduce my risk exposure by systematically selling in stages.

Calculating the odds

We have 76 years of market history at our disposal, which will allow us to answer the following questions:

1. Of the 19,800 days in our dataset, how frequently was the current price at least 40% below the most recent high-water mark? We’ll call these “super-bear days.”
2. Of the 19,800 days, how frequently was the current price at least 20% below the most recent high-water mark? We’ll call these “bear days.”
3. Of the 19,800 days, how frequently was the current price between 10% and 20% below the most recent high? We’ll call these “correction days.”
4. Of the 19,800 days, how frequently was the current price between 5% and 10% below the most recent high? We’ll call these “pullback days.”
5. Of the 19,800 days, how frequently was the current price within 5% of the most recent high? We’ll call these “benign days.”
6. And finally, of the 19,800 days, how many represented a new high-water mark? We’ll call these “happy days.”
7. What happens to the frequencies of these decline categories if we place a time limit of 12 months from today?
8. What if we limit the time frame to just 24 months?

To answer these questions, all we do is count. No advanced math, no algebra, no fancy formulas – just counting. This first step in the process is establishing the baseline probabilities.

The baseline probabilities

Let’s first define some terms.

• DD = Drawdown. The percent change in price from peak to trough over a given date range.
• DD Level = ranges of observed drawdowns, from less than 5% to more than 40%.
• # Days = the number of observations for each range.
• Probability = # Days divided by All Days (19,800).

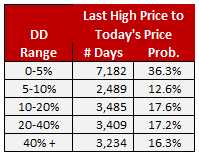
Table 1.

Table 1 shows the distribution of drawdowns across each of our categories, from benign to super-bear. Looking at the entire period from 1941-2017 we learn three things. First, the market has spent a little more than one-third of its’ days bouncing happily between new high-water marks and declines of less than 5%. Therefore, the baseline probability of any randomly selected day in the market being a “happy day” is 36.3%.

Second, the market has spent 12.6% of its’ days in the mildly anxious state between a pullback of 5% and the beginning of an official “correction” of 10%. Corrections get a lot of media attention. The thing that’s so worrisome about corrections is that you never know how far they will go or when they might stop. But don’t worry – we have the technology to find a credible answer to those questions.

Third, the market spent 17.6% of its’ days in the decidedly worrisome stage between a 10% correction and a 20% bear market. So many decisions to make, and so little time. Should you bail? Should you stand pat? Or should you just play a little defense by reducing your risk exposure in accordance with the probabilities of the drawdown getting much worse?

Fourth, the market has spent one-third of its’ days in bear market territory. This gives us our initial answer to the likelihood of being in a bear market on any randomly selected day – 33.5%. I say it’s an initial answer because we’re going to test it with Table 2 to find out if the numbers hold up.

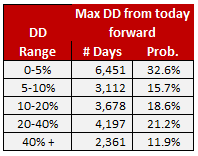
Table 2.

Table 2 looks at the historical data in a slightly different way. Table 1 used a backward-looking calculation of drawdowns, starting from the most recent high-water mark and ending with the current day’s price. Table 2 starts with the current price, and looks ahead to find the lowest price ever recorded from that day forward. This table answers a very different question than the one we asked of Table 1.

While Table 1 answers the question “how much lower is today’s price from the last high price?”, Table 2 answers the question “how far down did the market go from today’s price to the end of the data?” So, table 1 describes the current condition of the market, while table 2 describes the future condition of the market.

The probabilities in Tables 1 and 2 are very similar. This tells us that, no matter how you slice it, there’s a 33% baseline probability of being in a bear market on any given day. This is good information to have, but it’s not enough to give us a practical estimate of how risky things are right now. To do that, we take the next step, and adjust the baseline probability by considering other factors that have influence over the likelihood that a new bear market is coming. These factors are called conditional probabilities.

 Conditional probabilities

The first of these factors, or conditions, is time. In Tables 1 and 2 we placed no time limit on the arrival of a bear market. Today, for example, we haven’t had a bear market for almost 9 years. So we will now impose a limit of 12 months to our look-ahead time frame. This changes the question from “any randomly selected day” to “any day between today and 12 months from today.” This makes the answer more practical, because we are much more interested in what might happen in the next year, than we are about what might happen 3, 5, or 10 years from now.

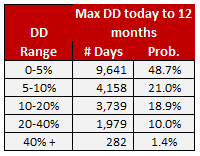
Table 3.

Table 3 is the same as the others, except we are only looking ahead 12 months. There are notable changes in the probabilities of various outcomes. Happy days become more prevalent – 48.7% instead of 33%. Bear markets are far less likely to arrive within the next 12 months. 11.4% instead of 33%. This is good news. We can now relax a little more, knowing that the odds have improved from 1-in-3, to 1-in-10 that a bear market is coming.

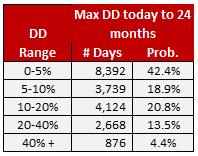
We do the same calculation in Table 4, this time using 24 months as our forward-looking time frame.

Table 4.

As expected, when we give the market more time to develop, the odds of a bear market go up, but are still lower than where we started. They are now 1-in-7, compared to 1-in-10 for the 12-month time frame. Let’s stop and review what we’ve learned about bear market probabilities thus far.

What did we learn from these tables?

1. On any given day in the market, there is a 33% chance of being in a bear market.
2. There is a similar chance, 33%, of experiencing a 20% decline from today’s price to some point in the future.
3. If we shorten the time frame to just the next 24 months, the risk of a bear market drops from 33% down to 18%. This makes sense, because bear markets do not follow a schedule. The less time we give them to develop, the less likely they become.
4. If we limit our time frame to just the next 12 months, the chances of encountering a new bear market drop from 33% all the way down to 11%. This, I believe, is the most relevant and practical measure of bear market risk for most investors.

Conclusions

Now that we know that the risk of a 20% drop in the market (a bear market) happening sometime in the next 12 months is 11.4%, how should we use this information? My opinion is that we should take it with a large grain of salt. Why? Because this probability is based on historical data. As important as history is, there is no guarantee that the future will unfold in a similar way.

To advance the accuracy of a bear market forecast, we must fine-tune our preliminary findings to account for other factors that have influenced the arrival of past bear markets. For example, economic recessions are virtually guaranteed to trigger a bear market. In the next part of this series we’ll look at the numbers in the context of past recessions.

Another factor of influence is the occurrence of a new high-water mark. Of the 19,800 days in our dataset, there have only been 1,070 high-water marks. That works out to 5.4% of all days. Wouldn’t it make sense to track what happens in the market after each of these events? We will do that.

Another factor is momentum. Specifically, downside momentum. This is a real thing in the stock market. Just as physics tells us that an object in motion tends to stay in motion, the same is true of stock prices. The question we will ask about momentum is this: do the odds of a bear market change when the market is already down by 5%? By 10%. This too is useful information.

There are other factors that influence the arrival of bear markets, but we will tackle them in a future chapter of this discussion. Be sure to check out my weekly series “Tracking the Market’s Undercurrents” here.

And check out this weird way to track undercurrents here.